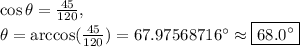Question

A projectile is fired with an initial velocity of 120 meters per second at an unknown angle above the horizontal. If the projectile's speed at the top of the trajectory is 45 meters per second, what is the unknown angle

Answer 1

`68.0^(\circ)`

Step-by-step explanation:

A projectile's vertical velocity at the top of its flight path must be zero, therefore the speed at the top of the trajectory must be referring to the object's horizontal velocity. Since there are exactly zero horizontal forces acting on the object, its horizontal velocity will remain the exact same throughout the entire launch. Thus, the horizontal component of the initial launch must be 45 meters per second, and we have the following equation using basic trigonometry for a right triangle:

Let
`\theta` be the unknown angle above the horizontal.

`\cos \theta=(45)/(120),\\\theta=\arccos((45)/(120))=67.97568716^(\circ)\approx \boxed{68.0^(\circ)}`