Question

A simple random sample of items resulted in a sample mean of . The population standard deviation is . a. Compute the confidence interval for the population mean. Round your answers to one decimal place. ( , ) b. Assume that the same sample mean was obtained from a sample of items. Provide a confidence interval for the population mean. Round your answers to two decimal places. ( , ) c. What is the effect of a larger sample size on the interval estimate? Larger sample provides a - Select your answer - margin of error.

Answer 1

(a): The 95% confidence interval is (46.4, 53.6)

(b): The 95% confidence interval is (47.9, 52.1)

(c): Larger sample gives a smaller margin of error.

Explanation:

Given

`n = 30` -- sample size

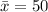`\bar x = 50` -- sample mean

`\sigma = 10` --- sample standard deviation

Solving (a): The confidence interval of the population mean

Calculate the standard error

`\sigma_x = (\sigma)/(\sqrt n)`

`\sigma_x = \frac{10}{\sqrt {30}}`

`\sigma_x = (10)/(5.478)`

`\sigma_x = 1.825`

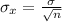
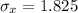
The 95% confidence interval for the z value is:

`z = 1.960`

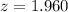
Calculate margin of error (E)

`E = z * \sigma_x`

`E = 1.960 * 1.825`

`E = 3.577`

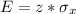
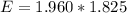
The confidence bound is:

`Lower = \bar x - E`

`Lower = 50 - 3.577`

`Lower = 46.423`

`Lower = 46.4` --- approximated

`Upper = \bar x + E`

`Upper = 50 + 3.577`

`Upper = 53.577`

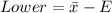
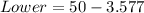
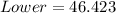
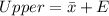
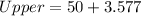
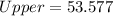
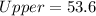`Upper = 53.6` --- approximated

So, the 95% confidence interval is (46.4, 53.6)

Solving (b): The confidence interval of the population mean if mean = 90

First, calculate the standard error of the mean

`\sigma_x = (\sigma)/(\sqrt n)`

`\sigma_x = \frac{10}{\sqrt {90}}`

`\sigma_x = (10)/(9.49)`

`\sigma_x = 1.054`

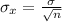
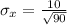
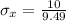
The 95% confidence interval for the z value is:

`z = 1.960`

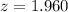
Calculate margin of error (E)

`E = z * \sigma_x`

`E = 1.960 * 1.054`

`E = 2.06584`

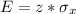
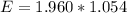
The confidence bound is:

`Lower = \bar x - E`

`Lower = 50 - 2.06584`

`Lower = 47.93416`

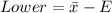
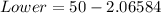
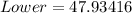
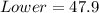`Lower = 47.9` --- approximated

`Upper = \bar x + E`

`Upper = 50 + 2.06584`

`Upper = 52.06584`

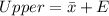
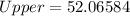
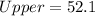`Upper = 52.1` --- approximated

So, the 95% confidence interval is (47.9, 52.1)

Solving (c): Effect of larger sample size on margin of error

In (a), we have:

`n = 30`
`E = 3.577`

In (b), we have:

`n = 90`
`E = 2.06584`

Notice that the margin of error decreases when the sample size increases.