Question

he owner of a local supermarket wants to estimate the difference between the average number of gallons of milk sold per day on weekdays and weekends. The owner samples 5 weekdays and finds an average of 259.23 gallons of milk sold on those days with a standard deviation of 34.713. 10 (total) Saturdays and Sundays are sampled and the average number of gallons sold is 365.12 with a standard deviation of 48.297. Construct a 90% confidence interval to estimate the difference of (average number of gallons sold on weekdays - average number of gallons sold on weekends). Assume the population standard deviations are the same for both weekdays and weekends.

Answer 1

90% confidence interval is ( -149.114, -62.666 )

Explanation:

Given the data in the question;

Sample 1 Sample 2

x"₁ = 259.23 x"₂ = 365.12

s₁ = 34.713 s₂ = 48.297

n₁ = 5 n₂ = 10

With 90% confidence interval for μ₁ - μ₂ { using equal variance assumption }

significance level ∝ = 1 - 90% = 1 - 0.90 = 0.1

Since we are to assume that variance are equal and they are know, we will use pooled variance;

Degree of freedom DF = n₁ + n₂ - 2 = 5 + 10 - 2 = 13

Now, pooled estimate of variance will be;

`S_p^2` = [ ( n₁ - 1 )s₁² + ( n₂ - 1)s₂² ] / [ ( n₁ - 1 ) + ( n₂ - 1 ) ]

we substitute

`S_p^2` = [ ( 5 - 1 )(34.713)² + ( 10 - 1)(48.297)² ] / [ ( 5 - 1 ) + ( 10 - 1 ) ]

`S_p^2` = [ ( 4 × 1204.9923) + ( 9 × 2332.6 ) ] / [ 4 + 9 ]

`S_p^2` = [ 4819.9692 + 20993.4 ] / [ 13 ]

`S_p^2` = 25813.3692 / 13

`S_p^2` = 1985.64378

Now the Standard Error will be;

`S_{x1-x2` = √[ (
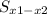`S_p^2` / n₁ ) + (
`S_p^2` / n₂ ) ]

we substitute

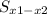`S_{x1-x2` = √[ ( 1985.64378 / 5 ) + ( 1985.64378 / 10 ) ]

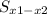`S_{x1-x2` = √[ 397.128756 + 198.564378 ]

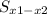`S_{x1-x2` = √595.693134

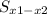`S_{x1-x2` = 24.4068

Critical Value =
`t_{(\alpha )/(2), df` =
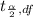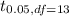`t_{0.05, df=13` = 1.771 { t-table }

So,

Margin of Error E =
`t_{(\alpha )/(2), df` × [ (
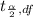`S_p^2` / n₁ ) + (
`S_p^2` / n₂ ) ]

we substitute

Margin of Error E = 1.771 × 24.4068

Margin of Error E = 43.224

Point Estimate = x₁ - x₂ = 259.23 - 365.12 = -105.89

So, Limits of 90% CI will be; x₁ - x₂ ± E

Lower Limit = x₁ - x₂ - E = -105.89 - 43.224 = -149.114

Upper Limit = x₁ - x₂ - E = -105.89 + 43.224 = -62.666

Therefore, 90% confidence interval is ( -149.114, -62.666 )