Answer:
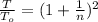
Step-by-step explanation:
This is a string resonance exercise, the wavelengths in a string held at the ends is
λ = 2L₀ / n
where n is an integer
the speed of the wave is
v = λ f
f = v /λ
the speed of the wave is given by the characteristics of the medium (string)
v =
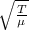
we substitute
f =
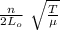
to obtain the following harmonic we change n → n + 1
f’ =
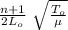
In this case, it tells us to change the tension to obtain the same frequency.
f ’= \frac{n}{2L_o} \ \sqrt{\frac{T}{\mu } }
how the two frequencies are equal
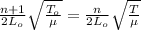
(n + 1)
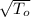 = n
= n
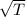

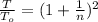
this is the relationship of the voltages to obtain the following harmonic,