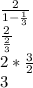Question

Find the the sum for the shown infinite geometric series?
2,2/3, 2/9, ...

Answer 1

3

Explanation:

The formula for the sum of an infinite geometric series is

`(a)/(1-r)`

Where a is the first term and r is the common ratio. We can see that the first term is 2, and to find the common ratio, we can divide a term by the one before it. We can get:

`((2)/(3))/(2) =(2)/(3) *(1)/(2)=(1)/(3)`

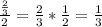
Now, we have all the values need to evaluate the formula. We can plug them in:

`(2)/(1-(1)/(3) ) \\(2)/((2)/(3) ) \\2*(3)/(2)\\3`