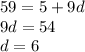Question

Find the common difference for an arithmetic series with
a1=5 and S10 = 320.

Answer 1

6

Explanation:

Let
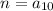`n = a_(10)`. We know the formula for the sum of an arithmetic sequence is:

`S_(n) = (n(a_(1)+a_(n) ))/(2)`

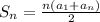
Where n is the number term you are finding the sum up to, a1 is the first term, and an is the nth term. We can substitute what we have:

`320=(10(5 + n))/(2)`

`640=10(n+5)\\64=n+5\\n=59`

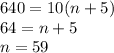
The formula to find the nth term of an arithmetic series is:

`a_(n) = a_(1) + (n-1)d`

Where d is the common difference. Again, we can plug in what we have;

`59 = 5 + 9d\\9d = 54\\d = 6`