Question

The population of a certain town is known to increase at a rate proportional to the current population. If the population doubles every 15 years, and the current population is 32,000, then what will be the population in 11 years g

Answer 1

The population in 11 years will be of 53,199.

Explanation:

Equation for a population that doubles every n years.

The population of an specie, after t years, considering that is doubles after n years, is given by an equation in the following format:

`P(t) = P(0)(2)^{(t)/(n)}`

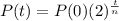
In which P(0) is the initial population.

The population doubles every 15 years, and the current population is 32,000

This means that
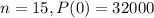`n = 15, P(0) = 32000`. So

`P(t) = P(0)(2)^{(t)/(n)}`

`P(t) = 32000(2)^{(t)/(15)}`

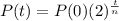
What will be the population in 11 years?

This is P(11). So

`P(t) = 32000(2)^{(t)/(15)}`

`P(11) = 32000(2)^{(11)/(15)}`

`P(11) = 53199`

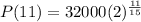
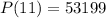
The population in 11 years will be of 53,199.