Question

If the half-life of Carbon-14 is 5700 years, how many years would it take a sample to decay from 1 gram to 31.3 mg

Answer 1

28500 years

Step-by-step explanation:

Applying,

A = A'(
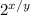`2^(x/y)`)............... Equation 1

Where A = Original mass of Carbon-14, A' = Final mass of carbon-14 after decaying, x = total time, y = half-life.

From the question,

Given: A = 1 g, A' = 31.3 mg = 0.0313 g, y = 5700 years.

Substitute these values into equation 1

1 = 0.0313(
`2^(x/5700)`)

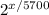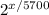`2^(x/5700)` = 1/0.0313

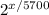`2^(x/5700)` = 31.95

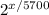`2^(x/5700)` ≈ 32

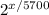`2^(x/5700)` ≈ 2⁵

Equating the base and solve for x

x/5700 ≈ 5

x ≈ 5×5700

x ≈ 28500 years