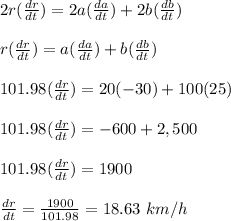Answer:
The rate of change of distance between the two ships is 18.63 km/h
Step-by-step explanation:
Given;
distance between the two ships, d = 140 km
speed of ship A = 30 km/h
speed of ship B = 25 km/h
between noon (12 pm) to 4 pm = 4 hours
The displacement of ship A at 4pm = 140 km - (30 km/h x 4h) =
140 km - 120 km = 20 km
(the subtraction is because A is moving away from the initial position and the distance between the two ships is decreasing)
The displacement of ship B at 4pm = 25 km/h x 4h = 100 km
Using Pythagoras theorem, the resultant displacement of the two ships at 4pm is calculated as;
r² = a² + b²
r² = 20² + 100²
r = √10,400
r = 101.98 km
The rate of change of this distance is calculated as;
r² = a² + b²
r = 101.98 km, a = 20 km, b = 100 km