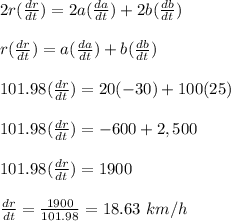Question

At noon, ship A is 140 km west of ship B. Ship A is sailing east at 30 km/h and ship B is sailing north at 25 km/h. How fast (in km/hr) is the distance between the ships changing at 4:00 p.m.

Answer 1

The rate of change of distance between the two ships is 18.63 km/h

Step-by-step explanation:

Given;

distance between the two ships, d = 140 km

speed of ship A = 30 km/h

speed of ship B = 25 km/h

between noon (12 pm) to 4 pm = 4 hours

The displacement of ship A at 4pm = 140 km - (30 km/h x 4h) =

140 km - 120 km = 20 km

(the subtraction is because A is moving away from the initial position and the distance between the two ships is decreasing)

The displacement of ship B at 4pm = 25 km/h x 4h = 100 km

Using Pythagoras theorem, the resultant displacement of the two ships at 4pm is calculated as;

r² = a² + b²

r² = 20² + 100²

r = √10,400

r = 101.98 km

The rate of change of this distance is calculated as;

r² = a² + b²

r = 101.98 km, a = 20 km, b = 100 km

`2r((dr)/(dt) ) = 2a((da)/(dt) ) + 2b((db)/(dt) )\\\\r((dr)/(dt) ) = a((da)/(dt) ) + b((db)/(dt) )\\\\101.98((dr)/(dt) ) = 20(-30 ) + 100(25 )\\\\101.98((dr)/(dt) ) = -600 + 2,500\\\\101.98((dr)/(dt) ) = 1900\\\\(dr)/(dt) = (1900)/(101.98) = 18.63 \ km/h`