Question

What is the vertex of this quadratic?

Answer 1

vertex = (3, 2 )

Explanation:

The vertex is the turning point of the graph.

This occurs at (3, 2 ) ← vertex

Answer 2

The vertex is at (3, 2)

Explanation:

Hello!

Vertex

The vertex of a parabola is the point of turning, or the minimum/maximum point of the parabola.

Since the graph opens up, the vertex is at the minimum point.

The y-value is 2, and the x-value is 3, giving us the vertex of (3, 2)

Other Parts

There are other parts to parabola than just the vertex.

Standard form of a quadratic:
`ax^2 + bx + c`

Other parts include:

• Axis of Symmetry, the line where the parabola is exactly symmetrical, and when folded in half, the sides will match. It is found using the formula
  `-(b)/(2a)`
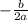
• X-intercepts, also known as the roots or zeroes of the graph, is where the graph touches the x-axis. It is found using the quadratic formula:
  `x = (-b\pm√(b^2 - 4ac))/(2a)`
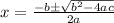
• Y-intercepts, the point where the graph hits the y-axis. It is the "b" value in the equation.