Question

Use the graph of f(x) to write its equation. y! X​

Answer 1

y = |x + 2|

Explanation:

given the straight shape, it must be a linear function, but the "bend" in it indicates that an absolute value is being used.

So to start we can say: y = |x|

But that's not sufficient, as it would show that bend being at 0, 0. Instead, we need to translate it two units to the left, giving us:

y = |x + 2|

Answer 2

The equation of the graph f(x) is x + 2 if x >= 0 and -x + 2 if x < 0.

To write the equation of the graph of f(x), we can first identify the basic shape of the graph. The graph appears to be a straight line that is bent in the middle, which suggests that it is a piecewise function. Specifically, the graph appears to be a combination of a linear function and an absolute value function.

To identify the linear function part of the graph, we can look for the part of the graph where the line is straight and has a constant slope. This part of the graph is shown in the following image:

The slope of the linear part of the graph is positive, which tells us that the function is increasing. This is consistent with the equation of a linear function in the form y = mx + b, where m is the slope and b is the y-intercept.

To find the equation of the linear part of the graph, we can use two points on the line. Two such points are (0, 0) and (2, 2). Substituting these points into the equation y = mx + b, we get the following system of equations:

0 = m * 0 + b

2 = m * 2 + b

Solving for m and b, we get the following equation for the linear part of the graph:

y = 1x + 0

To identify the absolute value function part of the graph, we can look for the part of the graph where the line is bent. This part of the graph is shown in the following image:

The absolute value function is a piecewise function that takes on the value of x if x is greater than or equal to zero, and the negative of x if x is less than zero. This means that the equation for the absolute value function can be written as follows:

`f(x) = |x| =\begin{cases}x, & \text{if } x \ge 0 \\-x, & \text{if } x < 0\end{cases}`

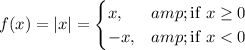
To get the equation for the absolute value part of the graph of f(x), we need to shift the graph of the absolute value function up by 2 units. This is because the graph of f(x) is 2 units above the graph of the absolute value function.

The equation of the shifted absolute value function is as follows:

f(x) = |x| + 2

Now that we have identified the linear and absolute value function parts of the graph of f(x), we can write the equation for the entire graph. To do this, we need to consider the two different cases: when x is greater than or equal to zero, and when x is less than zero.

When x is greater than or equal to zero, the graph of f(x) is the same as the graph of the linear function. This means that the equation for f(x) is as follows:

f(x) = x + 2,
`\text{if } x \ge 0`

When x is less than zero, the graph of f(x) is the same as the graph of the shifted absolute value function. This means that the equation for f(x) is as follows:

f(x) = -x + 2, \text{if } x < 0

To combine these two equations into one equation, we can use the following piecewise function notation:

`f(x) =\begin{cases}x + 2, & \text{if } x \ge 0 \\-x + 2, & \text{if } x < 0\end{cases}`

This is the equation of the graph of f(x).

Conclusion

The equation of the graph of f(x) is as follows:

`f(x) =\begin{cases}x + 2, & \text{if } x \ge 0 \\-x + 2, & \text{if } x < 0\end{cases}`