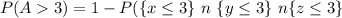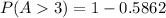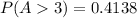Answer:
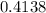
Explanation:
Given
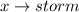



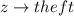
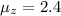
Let the event that the above three factors is greater than 3 be represented as:

Using complement rule, we have:
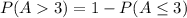
This gives:
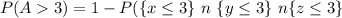
-----------------------------------------------------------------------------------------------------------
The exponential distribution formula of each is:
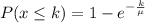
So, we have:
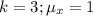
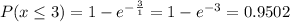
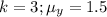
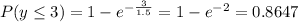
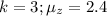
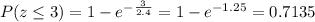
-----------------------------------------------------------------------------------------------------------