Given:
The height of ball is represented by the below function:
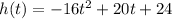
To find:
The number of seconds it will take to reach the ground.
Solution:
We have,
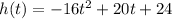
At ground level, the height of ball is 0, i.e.,
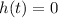 .
.
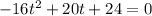
Taking out greatest common factor.
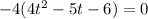
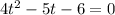
Splitting the middle term, we get
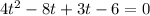
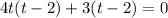
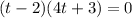
Using zero product property, we get
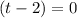 and
and
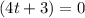
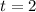 and
and

Time cannot be negative, so
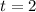 .
.
Therefore, the ball will reach the ground after 2 seconds.