Answer:
Explanation:
From the given information:
Null and alternative hypothesis is:
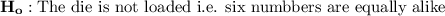
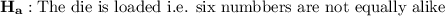
Numbers Observed Expected (O - E) (O-E)^2 (O-E)^2/E
Frequency (O) Frequency (E)
1 31 30 1 1 0.03
2 34 30 4 16 0.53
3 26 30 -4 16 0.53
4 16 30 -14 196 6.53
5 32 30 2 4 0.13
6 41 30 11 121 4.03
Total 180
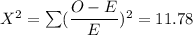
degree of freedom = n - 1
= 6 - 1
= 5
Critical value at
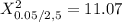
Since the calculated
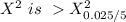 , then we reject
, then we reject
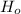
Conclusion: Accept the alternative hypothesis.
The information provided gives sufficient evidence for us to conclude that the given die is loaded.