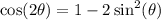Answers:
- cos(2theta) = -119/169
- cos(theta) = -5/13
=====================================================
The given info is:
- sin(theta) = 12/13
- theta is in quadrant II
From that, we can use the pythagorean trig identity to find that cos(theta) = -5/13. Keep in mind that cosine is negative in quadrant II.
Now use the trig identity below to compute cos(2theta)
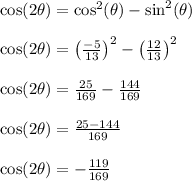
Other options you could use are these identities
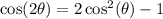
or