Question

Solve for 2. Round to the nearest tenth of a degree, if necessary, 7.2 D 10 9.4. B​

Answer 1

x=50°

use the sine rule to find the missing angle "x"

Answer 2

The value of angle DBC (x) is approximately 66.6 degrees.

To solve for x in the given triangle, we can use the cosine rule, which states that for any triangle with sides a, b, and c, and the angle opposite to side c is C, the following equation holds true:

`c^2 = a^2 + b^2 - 2ab * cos(C)`

In this case, we are given that angle DCB is 90 degrees, CB is 7.2, and DB is 9.4. We can use the cosine rule to find the value of angle DBC (which is equivalent to x).

Plugging in the given values, we get:

`9.4^2 = 7.2^2 + 7.2^2 - 2 * 7.2 * 7.2 * cos(DBC)`

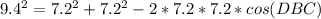
Solving for cos(DBC), we get:

cos(DBC) =
`(7.2^2 + 7.2^2 - 9.4^2) / (2 * 7.2 * 7.2)`

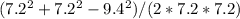
cos(DBC) ≈ 0.387

To find the value of DBC (x), we take the arccos of 0.387:

x ≈ arccos(0.387) ≈ 66.6 degrees

Therefore, the value of angle DBC (x) is approximately 66.6 degrees.