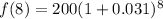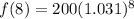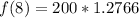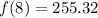Answer:
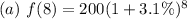
(b) After 8 years, the savings account has $255.32
Explanation:
Given
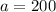 ---- initial (i.e. when t = 0)
---- initial (i.e. when t = 0)
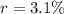
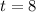
Solving (a): Model the situation
For growth, an exponential function is represented as:
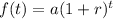
This gives:
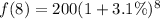
Solving (b): The solution to (a)
We have:
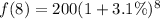
Express percentage as decimal