Question

Graph the image of ABC with vertices A(2,3), B(-4,4), C(-1,-3) after the glide reflection.

Translation:(x,y)—>(x+2,y)
Reflection: in the x-axis

Answer 1

Given:

The vertices of the triangle ABC are A(2,3), B(-4,4), C(-1,-3).

Translation:
`(x,y)\to (x+2,y)`

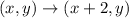
Reflection: in the x-axis.

To find:

The graph of the image.

Solution:

The vertices of the triangle ABC are A(2,3), B(-4,4), C(-1,-3).

The rule of translation is:

`(x,y)\to (x+2,y)`

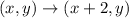
The points after translations are:

`A(2,3)\to A'(2+2,3)`

`A(2,3)\to A'(4,3)`

`B(-4,4)\to B'(-4+2,4)`

`B(-4,4)\to B'(-2,4)`

`C(-1,-3)\to C'(-1+2,-3)`

`C(-1,-3)\to C'(1,-3)`

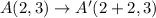
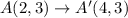
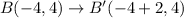
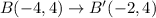
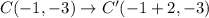
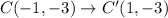
After that the figure is reflected across the x-axis. So, the rule of reflection is:

`(x,y)\to (x,-y)`

`A'(4,3)\to A''(4,-3)`

`B'(-2,4)\to B''(-2,-4)`

`C'(1,-3)\to C''(1,3)`

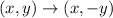
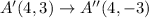
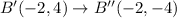
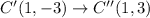
The vertices of image are A''(4,-3), B''(-2,-4), C''(1,3).