Given:
The vertices of the triangle ABC are A(2,3), B(-4,4), C(-1,-3).
Translation:
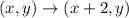
Reflection: in the x-axis.
To find:
The graph of the image.
Solution:
The vertices of the triangle ABC are A(2,3), B(-4,4), C(-1,-3).
The rule of translation is:
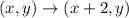
The points after translations are:
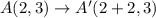

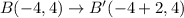
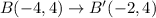
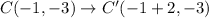
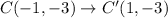
After that the figure is reflected across the x-axis. So, the rule of reflection is:
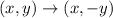
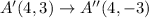
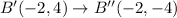
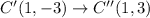
The vertices of image are A''(4,-3), B''(-2,-4), C''(1,3).