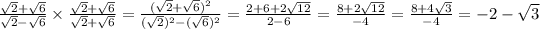Answer:

Explanation:
First consider numerator
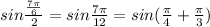
Using the formula : sin (A + B) = sin A cos B + cos A sin B
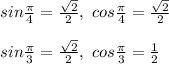
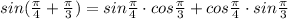
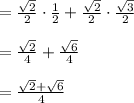
Second consider denominator
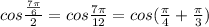
Using the formula : cos (A + B) = cos A cos B - sin A sin B
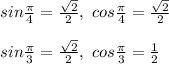
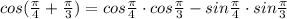
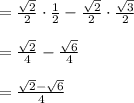
Therefore,
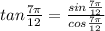
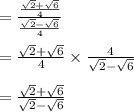
Either we can stop here or Rationalize the denominator: