Answer:
We proceed to demonstrate the identity given on statement by algebraic and trigonometric means:
1)
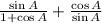 Given
Given
2)
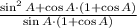
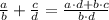 /Definition of power
/Definition of power
3)
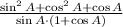 Distributive property/Definition of power
Distributive property/Definition of power
4)
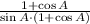 Associative property/
Associative property/
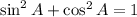
5)
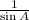 Existence of multiplicative inverse/Modulative property
Existence of multiplicative inverse/Modulative property
6)
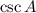
 /Result
/Result
Step-by-step explanation:
We proceed to demonstrate the identity given on statement by algebraic and trigonometric means:
1)
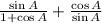 Given
Given
2)
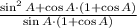
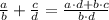 /Definition of power
/Definition of power
3)
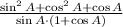 Distributive property/Definition of power
Distributive property/Definition of power
4)
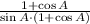 Associative property/
Associative property/
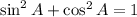
5)
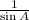 Existence of multiplicative inverse/Modulative property
Existence of multiplicative inverse/Modulative property
6)
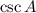
 /Result
/Result