Question

Which pair of functions are inverses of each other?

Wanting to make sure of answers in this pretest

Answer 1

The only pair of functions that are inverses of each other are the ones for option D.

Explanation:

Two functions, f(x) and g(x), are inverses if and only if:

f( g(x) ) = x

g( f(x) ) = x

So we need to check that with all the given options.

A)

`f(x) = (x)/(7) + 10 \\g(x) = 7*x - 10\\`

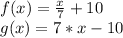
then:

`f(g(x)) = (7*x + 10)/(7) -10 = x + (10)/(7) - 10`

This is clearly different than x, so f(x) and g(x) are not inverses.

B)

`f(x) = \sqrt[3]{11*x} \\g(x) = ((x)/(11) )^3`

Then:

`f(g(x)) = \sqrt[3]{11*((x)/(11))^3 } = \sqrt[3]{(x^3)/(11^2) } = (x)/(11^(2/3))`

This is different than x, so f(x) and g(x) are not inverses.

C)

`f(x) = (7)/(x) -2 \\g(x) = (x + 2)/(7)`

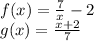
Then:

`f(g(x)) = (7)/((x + 2)/(7) ) - 2 = (7*7)/(x + 2) - 2`

Obviously, this is different than x, so f(x) and g(x) are not inverses.

D)

`f(x) = 9*x - 6\\g(x) = (x + 6)/(9)`

Then:

`f(g(x)) = 9*(x + 6)/(9) - 6 = x + 6 - 6 = x\\g(f(x)) = ((9*x - 6) + 6)/(9) = x`

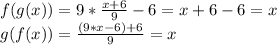
In this case we can conclude that f(x) and g(x) are inverses of each other.