Given:
In triangle UVW, X is the midpoint of UV and Y is the midpoint of VW.
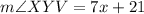

To find:
The measure of angle XYV.
Solution:
Since X is the midpoint of UV and Y is the midpoint of VW, therefore XY is the mid-segment of the triangle UVW and parallel to the base of the triangle, i.e., UW.
If a transversal line intersect two parallel lines, then the corresponding angles are congruent and their measures are equal.
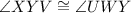 [Corresponding angle]
[Corresponding angle]
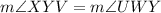
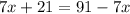
We need to solve this equation for x.
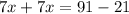
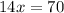
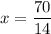

Now,
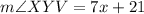
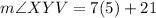
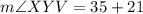
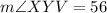
Therefore, the measure of angle XYV is 56 degrees.