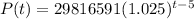Answer:
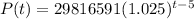
Explanation:
Equation:
The equation for the population of California, in t years after 1990, is given by:
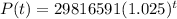
In which 29816591 is the initial population, that is, the population in 1990.
From 1995:
First, we have to find the population in 1995(5 years after 1990), which is P(5), which we will consider as the initial value in the equation.
So
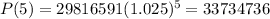
So
Since t is still given in years after 1990, we have to subtract t by 1995 - 1990 = 5 in the exponent. So