Question

In a survey 125 people, 90 people liked orange juice or grape juice. There are 62 people who like orange juice and 43 people who like grape juice. What is the probability that a randomly selected person likes both juices?

Answer 1

0.12 = 12% probability that a randomly selected person likes both juices.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

We solve this question treating these events as Venn probabilities.

I am going to say that.

Event A: Like orange juice.

Event B: Like grape juice.

In a survey 125 people, 90 people liked orange juice or grape juice.

This means that:

`P(A \cup B) = (90)/(125)`

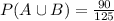
62 people who like orange juice and 43 people who like grape juice.

This means that:

`P(A) = (62)/(125), P(B) = (43)/(125)`

What is the probability that a randomly selected person likes both juices?

This is
`P(A \cap B)`, which is given by:

`P(A \cap B) = P(A) + P(B) - P(A \cup B)`.

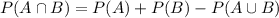With the values in this problem:

`P(A \cap B) = P(A) + P(B) - P(A \cup B) = (62)/(125) + (43)/(125) - (90)/(125) = (62 + 43 - 90)/(125) = (15)/(125) = 0.12`

0.12 = 12% probability that a randomly selected person likes both juices.