Question

Chromium 51 is a radioactive substance used in medicine. It has a 1/2 life of 28 days. The equation for its exponential decay model is `y=a(.5)^t/28 If 10 mg is ingested by a patient, how many days before only 8 mg is still emitting radiation?

Answer 1

9 days before only 8 mg is still emitting radiation.

Explanation:

The exponential model is:

`y(t) = a(0.5)^{(t)/(28)}`

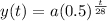
In which a is y(0), that is, the initial quantity.

10 mg is ingested by a patient

This means that
`a = 10`, and thus:

`y(t) = 10(0.5)^{(t)/(28)}`

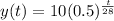
How many days before only 8 mg is still emitting radiation?

This is t for which y(t) = 8. So

`y(t) = 10(0.5)^{(t)/(28)}`

`8 = 10(0.5)^{(t)/(28)}`

`(0.5)^{(t)/(28)} = (8)/(10)`

`(0.5)^{(t)/(28)} = 0.8`

`\log{(0.5)^{(t)/(28)}} = \log{0.8}`

`((t)/(28))\log{0.5} = \log{0.8}`

`(t)/(28) = \frac{\log{0.8}}{\log{0.5}}`

`t = 28\frac{\log{0.8}}{\log{0.5}}`

`t = 9`

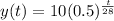
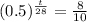
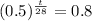
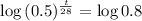
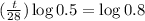
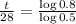
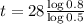
9 days before only 8 mg is still emitting radiation.