Answer:
f has no critical points.
Explanation:
We are given:

A function has critical points whenever its derivative equals 0 or is undefined.
Differentiate the function:

Since this will never be undefined, solve for its zeros:
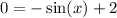
Hence:
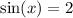
Recall that the value of sine is always between -1 and 1.
Thus, no real solutions exist.
Therefore, f has no critical points.