Part (a)
The graph is shown below. It's a piecewise function composed of 3 parts: Two flat horizontal segments and a decreasing segment.
Note the use of open holes at points C and E. They tell the reader that the specific point is not part of the function. For example, point C at (8000,0.75) is an open hole since the second piece has x = 8000 excluded. In other words, the domain for the second piece is
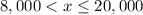 which says to exclude 8000 but to include 20,000.
which says to exclude 8000 but to include 20,000.
============================================================
Part (b)
The flat parts are due to the two first pieces being constant functions. Regardless of what x is on those portions, the cost per unit stays the same. We see that the cost starts off at 35 cents per unit (green segment), then it jumps to 75 cents per unit (blue segment).
So far the costs have been constant, but once we get to the red curve portion, then the costs decrease as x increases. Note that 1/(200,000) = 0.000005 which means the costs are decreasing by 0.000005 dollars per unit. Let's multiply that by 10,000 to get 10,000*0.000005 = 0.05
So for the red portion, the costs are decreasing by $0.05 per 10,000 units, or they are decreasing by 5 cents per 10,000 units. When x > 20000, the lowest we can get the cost is at 62 cents per unit. This is when production is at max capacity (42,000 units).
If you wanted the cost per unit to be as small as possible, and x didn't have to be larger than 20 thousand, then you'd stick to the green line. However, the drawback here is that you can only produce at max 8000 units.