The question is incomplete. The complete question is :
A long, straight wire lies along the z-axis and carries a 3.90-A current in the + z-direction. Find the magnetic field (magnitude and direction) produced at the following points by a 0.600 mm segment of the wire centered at the origin.
A) x=2.00m,y=0, z=0
Bx,By,Bz = ? T
Enter your answers numerically separated by commas.
B) x=0, y=2.00m, z=0
C) x=2.00m, y=2.00m, z=0
D) x=0, y=0, z=2.00m
Solution :
The expression of the magnetic field using the Biot Savart's law is given by :
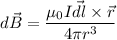
a). The position vector is on the positive x direction.
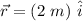
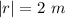
The magnetic field is
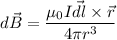
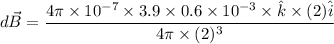
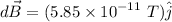
The magnetic field is
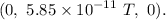
b). The position vector is in the positive y-direction.
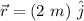
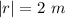
The magnetic field is
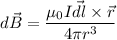
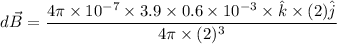
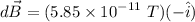
The magnetic field is
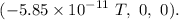
c). The position vector is :
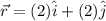
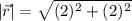
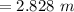
The magnetic field is
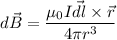
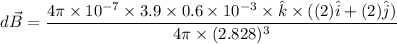
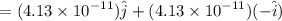
The magnitude of the magnetic field is :
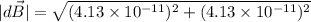
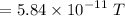
Therefore, the magnetic field is
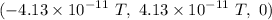
d). The position vector is in the positive y-direction.
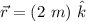
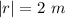
The magnetic field is
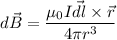
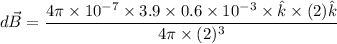
= 0 T
The magnetic field is (0, 0, 0)