The question is incomplete. The complete question is :
A circular loop of wire with a radius of 15.0 cm and oriented in the horizontal xy-plane is located in a region of uniform magnetic field. A field of 1.2 T is directed along the positive z-direction, which is upward. (a)If the loop is removed from the field region in a time interval of 2.8 ms, find the average emf that will be induced in the wire loop during the extraction process.
Solution :
Let us consider a
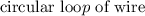 which has a
which has a
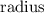 of r =
of r =
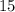 cm.
cm.
It is oriented horizontally along the xy-plane and is located in the region of an
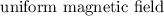 , such that it points in the positive z direction and having a magnitude of B = 1.2 T.
, such that it points in the positive z direction and having a magnitude of B = 1.2 T.
Now if the loop
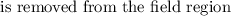 in a time interval of Δt = 2.8 ms. Initially the magnetic field and the area points is in the same direction, so that the angle between them is Ф = 0°, thus the initial and the final fluxes are :
in a time interval of Δt = 2.8 ms. Initially the magnetic field and the area points is in the same direction, so that the angle between them is Ф = 0°, thus the initial and the final fluxes are :
 and
and
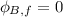
Area A =
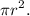 The induced emf equals to the change in the flux, and is divided by the time that it takes to go from the initial flux, Δt and multiplied by the number of turns N = 1, i.e. ,
The induced emf equals to the change in the flux, and is divided by the time that it takes to go from the initial flux, Δt and multiplied by the number of turns N = 1, i.e. ,
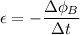
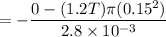
= 30.27 V
Therefore, the emf generated is 30.27 V.