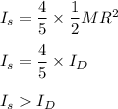Answer:
Step-by-step explanation:
In a Solid sphere; the moment of inertia around its geometrical axis can be expressed by using the formula:
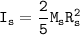
For the solid disk; the moment of inertia around the central axis is:
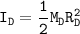
Suppose
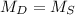 ; then we can say both to be equal to M
; then we can say both to be equal to M
As well as
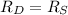 ; then that too can be equal to R
; then that too can be equal to R
Now;
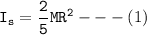

Multiplying equation (1) by 2, followed by dividing it by 2; we have: