Question

The sphere at the right fits snugly inside a cube with 18​-in. edges. What is the approximate volume of the space between the sphere and​ cube?

Answer 1

2,778 in³

Explanation:

Volume cube

v = 18³

v = 5,832

Volume sphere

v = (4/3)π9³

v = 3,053.6280592893

Volume space

v = 5,832 - 3,053.6280592893

v = 2,778.3719407107

2,778 in³

Answer 2

Explanation:

We need to first find the volume of the cube, then subtract from it the volume of the sphere. This is what we are being asked to find. First, the volume of the cube is length times width times height. Since this is a cube, all of the sides are the same length, making the volume

V = 18³ so

V = 5832 inches cubed. Now for the sphere.

The formula for the volume of a sphere is

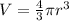`V=(4)/(3)\pi r^3` and we will use 3.1415 for π.

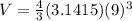`V=(4)/(3)(3.1415)(9)^3` which gives us

V = 3053.538

Subtracting the volume of the sphere from the volume of the cube:

V = 5832 - 3053.538

V = 2778.462 inches cubed