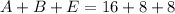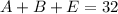Answer:
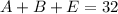
Explanation:
Given
![\int\limits {x^2\cdot e^(-4x)} \, dx = -(1)/(64)e^(-4x)[Ax^2 + Bx + E]C](https://img.qammunity.org/2022/formulas/mathematics/college/o57usqo7py833in0dy4rw1hn5c245kstp6.png)
Required
Find
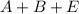
We have:
![\int\limits {x^2\cdot e^(-4x)} \, dx = -(1)/(64)e^(-4x)[Ax^2 + Bx + E]C](https://img.qammunity.org/2022/formulas/mathematics/college/o57usqo7py833in0dy4rw1hn5c245kstp6.png)
Using integration by parts
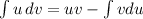
Where
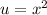 and
and
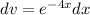
Solve for du (differentiate u)
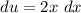
Solve for v (integrate dv)
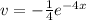
So, we have:
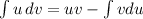
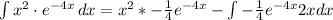
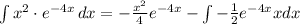
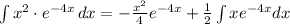
-----------------------------------------------------------------------
Solving
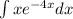
Integration by parts
 ----
----
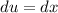
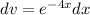 ----------
----------
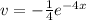
So:
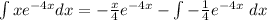
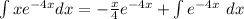
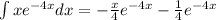
So, we have:
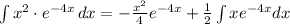
![\int\limits {x^2\cdot e^(-4x)} \, dx = -(x^2)/(4)e^(-4x) +(1)/(2) [ -(x)/(4)e^(-4x) -(1)/(4)e^(-4x)]](https://img.qammunity.org/2022/formulas/mathematics/college/o2cn23cx77tig3p7lms28aw7xb9m98n5lt.png)
Open bracket
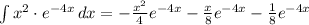
Factor out
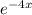
![\int\limits {x^2\cdot e^(-4x)} \, dx = [-(x^2)/(4) -(x)/(8) -(1)/(8)]e^(-4x)](https://img.qammunity.org/2022/formulas/mathematics/college/sc2cna79wlaqp3w373pulc2lqb2np7ur2q.png)
Rewrite as:
![\int\limits {x^2\cdot e^(-4x)} \, dx = [-(1)/(4)x^2 -(1)/(8)x -(1)/(8)]e^(-4x)](https://img.qammunity.org/2022/formulas/mathematics/college/17u21kdinyzg322sq2h2r1fxuqce15ulmr.png)
Recall that:
![\int\limits {x^2\cdot e^(-4x)} \, dx = -(1)/(64)e^(-4x)[Ax^2 + Bx + E]C](https://img.qammunity.org/2022/formulas/mathematics/college/o57usqo7py833in0dy4rw1hn5c245kstp6.png)
![\int\limits {x^2\cdot e^(-4x)} \, dx = [-(1)/(64)Ax^2 -(1)/(64) Bx -(1)/(64) E]Ce^(-4x)](https://img.qammunity.org/2022/formulas/mathematics/college/zsd0jk7q987ri2ga25qmvjjiqpp4kvxw0x.png)
By comparison:
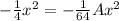
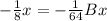
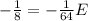
Solve A, B and C
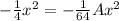
Divide by
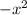
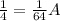
Multiply by 64
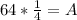
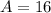
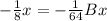
Divide by
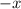
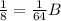
Multiply by 64
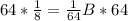
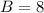
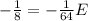
Multiply by -64
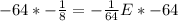
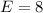
So: