Question

Si a los lados de un cuadrado se le aumenta en 3 y 5 m respectivamente la superficie del nuevo rectangulo es 440m .Encontrar el lado del cuadrado inicial

Answer 1

El lado del cuadrado inicial es 17 m.

Explanation:

El área de un rectángulo se calcula a partir de los dos lados diferentes. Siendo a y b el valor de ambos lados, el área de la figura es el producto de los dos lados contiguos del rectángulo.

A los lados de un cuadrado se le aumenta en 3 y 5 m respectivamente la superficie del nuevo rectángulo es 440 m². Siendo x el lado del cuadrado inicial, entonces el área del rectángulo se puede expresar como:

(x+3)*(x+5)= 440 m²

Resolviendo:

x*x + 5*x + 3*X + 3*5= 440

x² + 8*x + 15=440

x² + 8*x + 15 -440= 0

x² + 8*x -425= 0

Una función cuadrática de la forma a*x² + b*x + c= 0 se puede resolver mediante la expresión:

`\frac{-b+-\sqrt{b^(2)-4*a*c } }{2*a}`

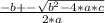
En este caso, a=1, b=8 y c=425. Reemplazando:

`\frac{-8+-\sqrt{8^(2)-4*1*(-425) } }{2*1}`

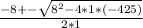
Resolviendo:

`\frac{-8+\sqrt{8^(2)-4*1*(-425) } }{2*1}= (-8+√(64+1700) )/(2*1)= (-8+√(1764 ) )/(2)= (-8+42 )/(2)= (34)/(2) = 17`

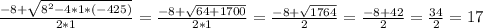
y

`\frac{-8-\sqrt{8^(2)-4*1*(-425) } }{2*1}= (-8-√(64+1700) )/(2*1)= (-8-√(1764 ) )/(2)= (-8-42 )/(2)= (-50)/(2) = -25`

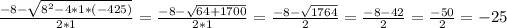
Como las longitudes no pueden ser negativas, el lado del cuadrado inicial es 17 m.