Question

What is the radius of polygon JKLMN ?

Answer 1

Radius of the circle is 5 units.

Explanation:

JKLMN is a regular polygon inscribed in a circle.

Since, its a regular polygon,

JN = NM = 5.88 units

"Perpendicular drawn from the center of the circle to any chord is the bisector of the chord"

Therefore, PQ will be the perpendicular bisector of chord NM.

QM =
`(1)/(2)(NM)`

QM =
`(1)/(2)(5.88)`

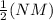
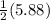
QM = 2.94 units

By applying Pythagoras theorem in ΔPQM,

PM² = PQ² + QM²

PM² = (4.05)² + (2.94)²

PM =
`√(16.4025+8.6436)`

PM =
`√(25.0461)`

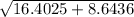
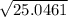
PM = 5 units

Therefore, radius of the circle is 5 units.