Answer:
Explanation:
In order for a company to break even, it earns no profit but it also incurs no loss. In other words, set the quadratic equal to 0 and factor to find x.
If you factor this using the quadratic formula you will get that the number of cars sold for the company to neither earn nor lose money is 1 or 21. Right in the middle is where we will find the maximum value (the vertex). This max value will give us the number of cars sold, h, and its corresponding value, k.
To solve for h easily, use the formula
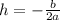 where a and b are the coefficients found in the standard form of a polynomial
where a and b are the coefficients found in the standard form of a polynomial
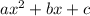 :
:
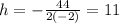 and for k, use:
and for k, use:
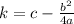 :
:
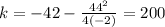
This means our vertex is (11, 200) and in the context of our problem, we know that when the company sells 11,000 cars it makes a max profit of 200 million dollars.