Answer:
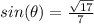
Explanation:
We know that:
sin(x)^2 + cos(x)^2 = 1
And we know that:
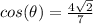
We want to find the value of the sine function evaluated in theta.
If we replace that in the first equation, we get:
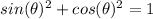
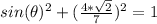
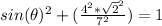
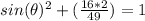
Now we can just isolate the sine part of that equation, so we get:

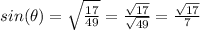
(We can't simplify the fraction anymore)