Answer:
1. Even Degree
2. 6 zeros
Explanation:
Determine if it’s an odd or even degree:—
- The graph is shown approach positive infinity when both sides of x-values, negative and positive, both approach their respective infinity sides.
To put it simply, see when both negative x-values and positive x-values approach their negative or positive infinity, the y-values will always be positive, even if negative x-values approach negative infinity.
For a polynomial function to be an even degree, it must satisfy the following:—
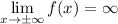
As an odd degree, either negative or positive x-values will approach positive infinity or negative infinity, depending on the function itself.
From the graph, we can say that the function is an even degree.
__________________________________________________________
Summary I
Even-Odd Degree
Even Degree, when both sides of x-value approach their respective infinity, y-value will always approach positive infinity.
Odd Degree, one side of y-value will approach positive infinity and another will approach negative infinity.
__________________________________________________________
Determine numbers of zeros:—
- We can determine numbers of zeros by examining x-axis and the graph. How many times does the graph intersect or pass through x-axis? Count and you should get 6 intercepts.
Therefore, there are 6 real solutions/zeros for this function/equation.
__________________________________________________________
Summary II
Determine zeros
To determine or check how many solutions or zeros do the graph/function/equation has, you can use the graph method. Simply count how many times does the graph pass through x-axis and x-intercepts are zeros.
__________________________________________________________
If you have any doubts regarding my answer or explanation, do not hesitate to ask in comment!