Answer:
Option 2: -¾
Explanation:
First identify 2 points on the line.
(0, 1), (4, -2)
Substitute the coordinates into the gradient formula below:
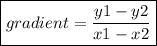
☆ (x₁, y₁) is the 1st coordinate and (x₂, y₂) is the 2nd coordinate.
Slope of the line
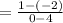
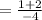
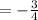
☆ Since the line is sloping downwards looking from the left to right, the line must have a negative slope.