Question

3.a circle of radius 5 units passes through the points (- 3,3) and (3,1) .

i.how many circles can be drawn that meet the given criteria?
ii. what can be the centre of a circle(S)
b. the equation of any two diameters of a circle are given by the straight lines x-y-4=0 and 2x+ 3y + 7 =0.
find the equation of the circle if it passes through the point (2,4).​

Answer 1

• See below

Explanation:

Given:

• Points (- 3,3) and (3,1) on a circle
• r = 5

i.

There are possible two points that can have a distance of 5 units from both of the given points, so possible two centers, hence two possible circles.

ii.

Let the points are A and B and the centers of circles are F and G.

The midpoint of AB, the point C is:

• C = ((-3 + 3)/2, (3 + 1)/2) = (0, 2)

The length of AB:

• AB =
  `√((3 + 3)^2 + (1 - 3)^2) = √(6^2+2^2) = √(40) = 2√(10)`

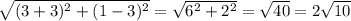
The distance AC = BC = 1/2AB =
`√(10)`

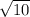
The distance FC or GC is:

• FC = GC =
  `√(5^2-10) = √(15)`

Possible coordinates of center are (h, k).

We have radius:

• (h + 3)² + (k - 3)² = 25
• (h - 3)² + (k - 1)² = 25

Comparing the two we get:

• (h + 3)² + (k - 3)² = (h - 3)² + (k - 1)²

Simplifying to get:

• k = 3h + 2

We consider this in the distance FC or GC:

• h² + (k - 2)² = 15
• h² + (3h + 2 - 2)² = 15
• 10h² = 15
• h² = 1.5
• h = √1.5 or
• h = - √1.5

Then k is:

• k = 3√1.5 + 2 or
• k = -3√1.5 + 2

So coordinates of centers:

• (√1.5, 3√1.5 + 2) for G or
• (√1.5, 3√1.5 + 2) for F (or vice versa)

-------------------------------------------------------------------------------------

b.

Diameters:

• x - y - 4 = 0
• 2x + 3y + 7 = 0

The intercession of the diameters is the center. We solve the system above and get. Not solving here as it is already a long answer:

• x = 1, y = -3

The point (2, 4) on he circle given.

Find the radius which is the distance between center and the given point:

• r =
  `√((2 - 1)^2+(4+3)^2) = √(1^2+7^2) = √(50)`

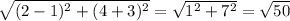
The equation of circle:

• (x - 1)² + (y + 3)² = 50