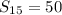Answer:
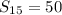
Explanation:
Given
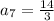
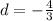

Required
The sum of n terms
First, we calculate the first term using:
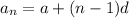
Let
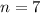
So, we have:
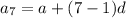
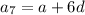
Substitute
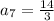 and
and
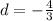
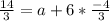
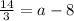
Collect like terms
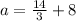
Take LCM and solve
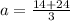
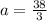
The sum of n terms is then calculated as:
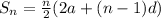
Where:

So, we have:
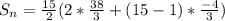
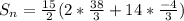
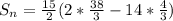
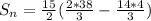
Take LCM
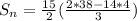
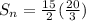
Open bracket
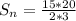
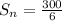
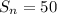
Hence,