Answer:
The half-life for the zombie population is of 8 years.
Explanation:
Exponential equation:
An exponential equation has the following format:
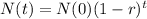
In which N(0) is the initial value and the part
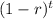 is related to the decay.
is related to the decay.
In this question:
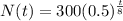
Thus N(0) = 300, that is, initial population of 300.
What is the half-life for the zombie population?
This is t for which N(t) = 0.5*300 = 150. So
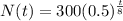
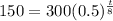
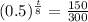
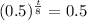
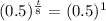
Equal exponents, so:
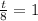
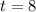
The half-life for the zombie population is of 8 years.