Question

FOR TRAN HERE YOU GO

Answer 1

Explanation:

(B) L = 182.9 cm +- 0.1 cm

W = 152.4 cm +- 0.1 cm

(C)

Smallest dimensions possible:

L = 182.9 cm - 0.1 cm = 182.8 cm

W = 152.4 cm - 0.1 cm = 152.3 cm

A = (182.9 cm)(152.3 cm)

= 27840.44 cm^2

To find the uncertainty for the area ∆A, we use the formula

`(da)/(a) = (dl)/(l) + (dw)/(w)`

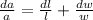
where da = ∆A, dl = ∆L, dw = ∆W

`\frac{da}{27840.44 {cm}^(2) } = (0.1cm)/(182.8cm) + (0.1cm)/(152.3cm)`

`= 0.000547 + 0.000657`

`= 0.001204`

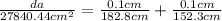
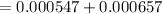
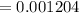
Therefore

∆A = 0.001204 × 27840.44 cm^2

= 33.52 cm^2

Rounding off the numbers to their significant figures,

A = 27840 cm^2 +- 33 cm^2

(D)

For the largest possible area,

L = 183.0 cm

W = 152.5 cm

A = 27905.5 cn^2

`\frac{da}{27907.5 {cm}^(2) } = (0.1cm)/(183.0cm) + (0.1cm)/(152.5cm)`

`= 0.001202`

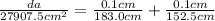
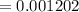
∆A = 0.001202 × 27907.5 cm^2

= 33.55 cm^2

Therefore, the largest possible area is

A = 27910 cm^2 +- 33 cm^2