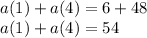Question

The function a(n) = 3(2)^n represents the value of the nth term in a sequence. What is the sum of the 1st and 4th terms of the sequence

Answer 1

54

Explanation:

We are given the sequence or function:—

`\displaystyle \large{a(n) = 3(2)^n}`

To find the sum of 1st term and 4th term, first we must find the first term and the fourth term which can be done by substituting n = 1 and n = 4.

`\displaystyle \large{a(1)=3(2)^1}\\\displaystyle \large{a(1)=3 \cdot 2}\\\displaystyle \large{a(1)=6}`

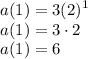
Then when n = 4.

`\displaystyle \large{a(4) = 3(2)^4}\\\displaystyle \large{a(4) = 3 \cdot 16}\\\displaystyle \large{a(4) = 48}`

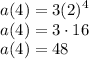
Therefore, the sum of 1st term and 4th term is:—

`\displaystyle \large{a(1)+a(4) = 6+48}\\\displaystyle \large{a(1)+a(4)=54}`