Question

Two companies modeled their profits for one yeor Which stotement describes the relationship between the profits, predicted by the models of the two companies?

Answer 1

The question is incomplete. The complete question is :

Two companies modeled their profits for one year.

• Company A used the function P(t)=1.8(1.4)^t to represent its monthly profit, P(t), in hundreds of dollars, after t months, where 0 < t ≤ 12.

• Company B used the data in the table to write a linear model to represent its monthly profits.

Which statement describes the relationship between the profits, predicted be the models, of the two companies?

Solution :

For one year, the two companies A and B modeled their profits.

It is given that :

Company A uses function
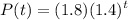`$P(t) = (1.8)(1.4)^t$` in order to represent the monthly profit of the company in hundreds of dollars after a time
`t`.

But the company B uses the data in the table in order to write the linear model to represent their monthly income.

We know the linear function is given by :

`$P(t)=mt+c$`

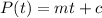
Here, m = slope of line

c = y-intercept

According to the data from the table , we see that the two points
`(3.5)` and
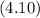`(4.10)` lies on the line so that the slope of the line is represented by :

`$(y-y')/(x-x')=(10-5)/(4-3)=5$`

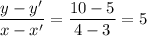
The point
`(3.5)` passes through the given line.

∴
`$5=5(3)+c$`

`$5=15+c$`

`$c=5-15$`

`$c=-10$`

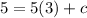
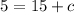
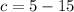
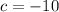
Therefore, the function will be
`$P(t) = 5t-10$`

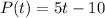
So, at
`t=4`,

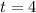the profit of the company A is
`$P(4)=(1.8)(1.4)^4$`

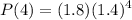
= 6.91

the profit of the company A is
`$P(4)=5(4)-10$`

= 20 - 10

= 10

Therefore,
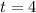`t=4`, the profit of the company B is more than the profit of company A.

Now at
`t=12`,

Profit of company A is
`$P(12) =(1.8)(1.4)^(12)$`

= 102.05

Profit of company B is
`P(12)=5(12)-10`

`$=66-10$`

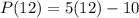
= 56

Therefore, the profit of company A is more that that of company B at the end of the year one.

Thus, company B had a greater profit for the fourth month and ended the year with the greater monthly profits than company A.

Option (B) is the correct answer.