Question

What is the radius of a hemisphere with a volume of 45729 in, to the nearest tenth
of an inch?

Answer 1

Explanation:

Use the volume of a sphere formula and then multiply it by .5 to get half of it, since a hemisphere is half of a sphere. Doing that gives us the formula:

`V=(4)/(3)\pi r^3(1)/(2)` which simplifies to

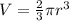`V=(2)/(3)\pi r^3` . Now, filling in what we were given:

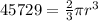`45729=(2)/(3)\pi r^3` which simplifies a bit to

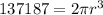`137187=2\pi r^3`. We divide by 2π to get

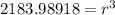`2183.98918=r^3` and take the cubed root on your calculator to get that

r = 27.9"

Answer 2

✏Answer:

`Volume= 45729in^3\\\\`

`Radius=r`

`2/3\pi r^3=45729`

`r^3=3*45729\\~~~~------\\~~~~~~2*3.14`

`r^3=21845.06`

`r=27.95~in`

✂-------------

hope it helps...

have a great day!!