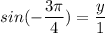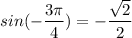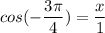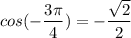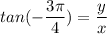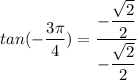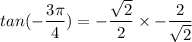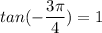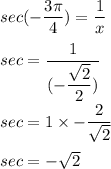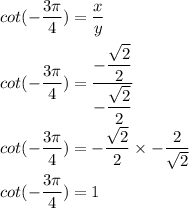Answer:
Explanation:
Let's take a look at the given angle 135°
The sketch of the angle which corresponds to
 unit circle and can be seen in the attached image below;
unit circle and can be seen in the attached image below;
The trigonometric ratios are as follows for an angle θ on the unit circle:
Trigonometric ratio related ratio on coordinate axes
sin θ
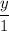
cos θ

tan θ
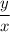
csc θ

sec θ

cot θ

From the sketch of the image attached below;
The six trigonometric ratio for 135° can be expressed as follows: