Question

At what temperature will uranium hexafluoride , the densest gas known have the same average speed as a molecule of the lightest gas, hydrogen at 37 degree celcius

Answer 1

the required temperature of uranium hexafluoride is 54156.25 K

Step-by-step explanation:

Given the data in the question;

We know that average speed is;

u =
`[ 3RT / MM ]^{1/2` ----------- let this be equation 1

where MM is the molar mass

T is temperature

R is universal gas constant and u is the average speed.

First we get the average speed of H₂

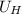`U_(H)`₂ =
`[ 3RT_H_2 / MM_H_2 ]^{1/2` ------ let this be equation 2

Next is the average speed of UF₆

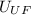`U_{UF`₆ =
`[ 3RT_(UF_6) / MM_(UF_6) ]^{1/2` ------ let this be equation 3

given that; both have the same average speed, equation 2 = equation 3;

`[ 3RT_H_2 / MM_H_2 ]^{1/2` =
`[ 3RT_(UF_6) / MM_(UF_6) ]^{1/2`

we multiply both sides by 1/3R and also square both sides.

`[ T_H_2 / MM_H_2 ]` =
`[ T_(UF_6) / MM_(UF_6) ]`

given that; temperature of hydrogen T
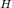`_{H`₂ = 37°C = ( 37 + 273.15)K = 310.15 K

we know that Molar mass of H₂; MM
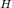`_{H`₂ = 2.016 g/mol

and molar mass of UF₆; MM
`_{UF`₆ = 352.02 g/mol

so we substitute

[ 310.15 K / 2.016 g/mol ] = [ T
`_{UF`₆ / 352.02 g/mol ]

T
`_{UF`₆ = [ 352.02 g/mol × 310.15 K ] / 2.016 g/mol

T
`_{UF`₆ = 109179.003 K/ 2.016

T
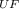`_{UF`₆ = 54156.25 K

Therefore, the required temperature of uranium hexafluoride is 54156.25 K