Question

Two events are observed in a frame of reference S to occur at the same space point, the second occurring 1.80 s after the first. In a frame S′ moving relative to S, the second event is observed to occur 2.05 s after the first. What is the difference between the positions of the two events as measured in S^?

Answer 1

The difference between the positions of the two events as measured in = 3.53 *10^8 m/s

Step-by-step explanation:

As we know -

`\Delta x = -\gamma \mu\Delta t`

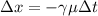
Here,

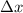`\Delta x` is the difference between the positions of the two events as measured in S^

`\gamma`
`= \frac{1}{\sqrt{1-(\mu^2)/(c^2) } }`

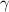
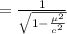
And

`\mu` = 0.547 c

Substituting the given values in above equation, we get -

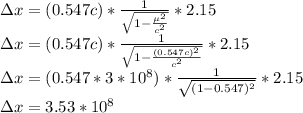`\Delta x = (0.547 c)*\frac{1}{\sqrt{1-(\mu^2)/(c^2) } }*2.15\\\Delta x = (0.547 c)*\frac{1}{\sqrt{1-((0.547 c)^2)/(c^2) } }*2.15\\\Delta x = (0.547 *3*10^8)*(1)/(√((1-\(0.547 )^2 ) )*2.15\\\Delta x = 3.53 *10^8`meter per second